在哪个卦限(在那个拐角处作文)

坐标系是一个超级伟大的发明在哪个卦限，它的出现把数学中的数与形紧密地结合在一起。

那么它是怎么被发明的呢在哪个卦限？相传有一天在哪个卦限，笛卡尔（Descartes 1596—1650在哪个卦限，法国哲学家、数学家、物理学家）生病卧床，牛人就是牛人，但他头脑一直没有休息，在反复思考一个问题：几何图形是直观的，而代数方程则比较抽象，能不能用几何图形来表示方程呢？这里，关键是如何把组成几何的图形的点和满足方程的每一组“数”挂上钩。他就拼命琢磨。通过什么样的办法、才能把“点”和“数”联系起来。突然，他看见屋顶角上的一只蜘蛛，拉着丝垂了下来，一会儿，蜘蛛又顺着丝爬上去，在上边左右拉丝。蜘蛛的“表演”，使笛卡尔思路豁然开朗。他想，可以把蜘蛛看做一个点，它在屋子里可以上、下、左、右运动，能不能把蜘蛛的每个位置用一组数确定下来呢？他又想，屋子里相邻的两面墙与地面交出了三条直线，如果把地面上的墙角作为起点，把交出来的三条线作为三根数轴，那么空间中任意一点的位置，不是都可以用这三根数轴上找到的有顺序的三个数来表示吗？反过来，任意给一组三个有顺序的数，例如3、2、1，也可以用空间中的一个点 P来表示它们。同样，用一组数（a， b）可以表示平面上的一个点，平面上的一个点也可以用一组二个有顺序的数来表示。于是在蜘蛛的启示下，笛卡尔创建了直角坐标系。

在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系，简称直角坐标系（Rectangular Coordinates）。通常，两条数轴分别置于水平位置与垂直位置，取向右与向上的方向分别为两条数轴的正方向。水平的数轴叫做x轴（x-axis）或横轴，垂直的数轴叫做y轴（y-axis）或纵轴，x轴y轴统称为坐标轴，它们的公共原点O称为直角坐标系的原点（origin）。

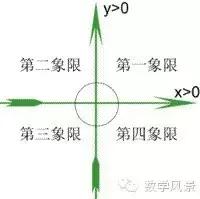
x轴y轴将坐标平面分成了四个象限（quadrant），右上方的部分叫做第一象限，其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限。还可以写成Ⅰ、Ⅱ、Ⅲ、Ⅳ。

过空间定点O作三条互相垂直的数轴，它们都以O为原点，具有相同的单位长度。这三条数轴分别称为x轴（横轴）、y轴（纵轴）、z轴（竖轴），统称为坐标轴。各轴之间的顺序要求符合右手法则，即以右手握住Z轴，让右手的四指从X轴的正向以90度的直角转向Y轴的正向，这时大拇指所指的方向就是Z轴的正向。这样的三个坐标轴构成的坐标系称为右手空间直角坐标系。与之相对应的是左手空间直角坐标系。一般在数学中更常用右手空间直角坐标系，在其他学科方面因应用方便而异。

三条坐标轴中的任意两条都可以确定一个平面，称为坐标面。它们是：由x轴及y轴所确定的xOy平面；y轴与z轴所确定的yOz平面；z轴与x轴所确定的zOx平面。这三个相互垂直的坐标面把空间分成八个部分，每一部分称为一个卦限．位于x，y，z轴的正半轴的卦限称为第一卦限，从第一卦限开始，在xOy平面上方的卦限，按逆时针方向依次称为第一、二，三，四卦限；下方的卦限依次称为第五，六，七，八卦限。也可以记作Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ与Ⅷ。

在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系，简称直角坐标系（Rectangular Coordinates）。通常，两条数轴分别置于水平位置与垂直位置，取向右与向上的方向分别为两条数轴的正方向。水平的数轴叫做x轴（x-axis）或横轴，垂直的数轴叫做y轴（y-axis）或纵轴，x轴y轴统称为坐标轴，它们的公共原点O称为直角坐标系的原点（origin）。

x轴y轴将坐标平面分成了四个象限（quadrant），右上方的部分叫做第一象限，其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限。还可以写成Ⅰ、Ⅱ、Ⅲ、Ⅳ。

那么问题来了，象限的英文是quadrant，‘quadr-’是表示‘四’的前缀；卦限的英文是octant，‘octa-’是表示‘八’的前缀。当初翻译者是如何考虑的，不是意译也不是音译，那翻译者的初衷是什么？

”象“不容易想，“卦”是很容易想的，八卦嘛！这样就很容易猜出当初译者的苦心了，《易传》有云：“易有太极，是生两仪，两仪生四象，四象生八卦，八卦定吉凶，吉凶生大业。” 当然更广泛地说法是太极生两仪，两仪生四象，四象生八卦。“象限”“卦限”正是出自于易经中的四象和八卦，很高大上的命名吧！

两条坐标轴（阴阳）造化了“四象”（天地之道，以阴阳二气造化万物），于是被称为“象限”。在空间解析几何中，三个坐标面把空间分为八部分，每一部分也因此被称为一个“卦限”。特别的空间坐标系中各个卦限的符号：I: +++，II: -++，III: –+，IV: +-+，V: ++-，VI: -+-，VII: —，VIII: +–，如果“+”用“——”表示，“-“用”— —“表示，那么正好对应八卦中的乾、兑、震、离、巽、坎、坤、艮。

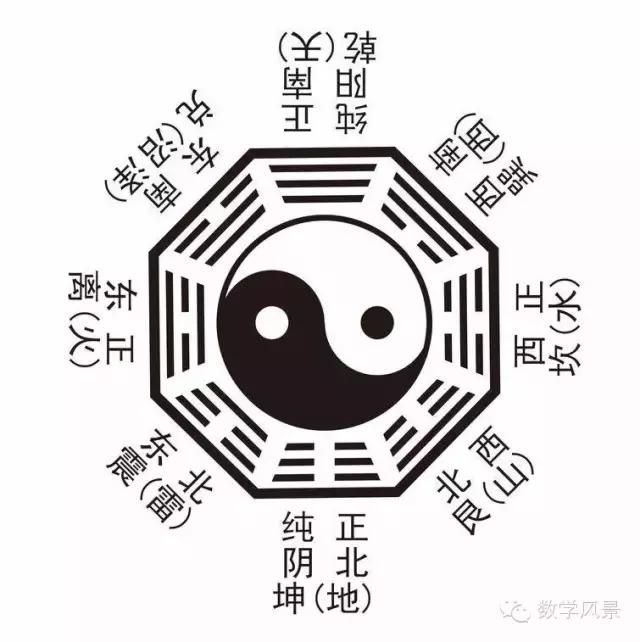
这是数学与国学的完美结合。

了解“象限”“卦限”的来历，虽然不能帮我们更好地学习数学，但了解一下还是有必要的，你会发现这是数学与传统国学的一次完美的结合，你会发现，生活中处处充满着乐趣，处处饱含着文化。

跟着我，你会发现数学越来越有意思！！