本篇文章给各位网友带来的资讯是:从氢原子到氢分子,《张朝阳的物理课》探究双原子分子振动转动光谱 详情请欣赏下文
2 月 11 日 12 时,《张朝阳的物理课》第二十七期准时开播。搜狐创始人、董事局主席兼 CEO 张朝阳坐镇搜狐视频直播间,探究双原子分子气体。张朝阳先带着网友复习氢原子薛定谔方程,根据求解得到的能级公式,讨论氢原子的光谱。接着研究两个氢原子组成的氢分子,其电子组成共价键将原子核束缚起来,将此势能在平衡位置展开得到等效的谐振子势,求解对应的薛定谔方程,解得包含振动与转动自由度的能级,通过此分立的能级与选择定则分析氢分子的光谱。

“我们学了那么多理论,解了那么多方程,现在需要应用一下。”张朝阳开门见山,“我们跟氢原子作战了很长时间,今天要讲氢分子,解决双原子分子气体问题。”
氢原子光谱与里德伯常量
他先带着网友,复习氢原子的薛定谔方程,求解得到氢原子的分立能级公式。

他说,“有了能级公式,就可以研究氢原子在各能级之间跃迁所产生的光谱。”通过推导,网友们发现,从初态能级到末态能级跃迁时,发射出的光线的波数为:
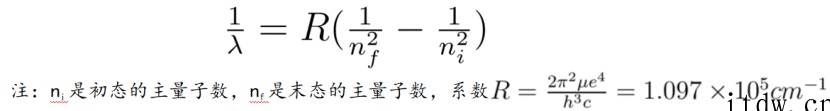
张朝阳解释说,“系数 R 称为里德伯常量,是量子力学出现之前,人们根据实验测得的氢原子光谱,抽象出的经验公式里得到的,这与用薛定谔方程计算的数值一致。”
他进一步解释,当末态主量子数为 1 时,末态就是基态,从各激发态到基态的跃迁形成的光谱就是莱曼系,它处于紫外光谱区。当末态主量子数为 2 时,更高激发态到末态的跃迁形成的光谱是巴尔末系,此线系处于可见光谱区,所以首先被发现。以此类推,可以得到其它谱系。
解薛定谔方程得到氢原子能级,导出的光谱与实验相符,重现了量子力学出现之前的各种线系,他说,“这证明了薛定谔方程的正确性。”
求解氢分子原子核的薛定谔方程
讨论完氢原子的光谱,再来讨论由氢原子组成的氢分子的情况。
“氢分子体系比氢原子复杂多了,它包含了两个氢原子核与两个电子,这四个粒子之间两两都有库伦势相互作用,直接解对应的薛定谔方程非常复杂。”张朝阳指出推导的难度所在和解决方案,“不过,由于电子质量远远小于原子核的质量,分子中电子速度远远大于原子核速度,所以当研究氢分子的振动和转动时,可以把电子看成一种分布,原子核沉浸在这种云一样的分布之中,电子云使得原子核之间具有某种有效的相互作用,从而将原子核结合在一起,这就是所谓的共价键。两个电子是两个原子所共有的。”
经推导发现,这种相互作用与原子核之间的库仑力一起,组成总的有效势能,若振幅较小,可将总有效势能在平衡位置附近做近似展开,得到谐振子势能,那么,重复之前得到的氢原子与谐振子的径向薛定谔方程的步骤,则可得出对应的氢分子中两原子核的径向薛定谔方程:
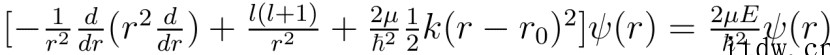
注:μ 是两个原子核的约化质量,r 是两原子核的距离,r0 是有效势能的平衡位置,l 是对应于角向波函数的角动量,k 是将有效势能在平衡位置附近展开时二次项的系数。由于这里只想讨论转动与振动能量,为了方便忽略了平衡位置时的势能项。

▲ (求解氢分子原子核径向薛定谔方程)
此时,张朝阳先根据解氢原子与谐振子径向薛定谔方程的经验,定义新的函数 u 为:
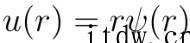
再代入到薛定谔方程之中,并将其化简为:
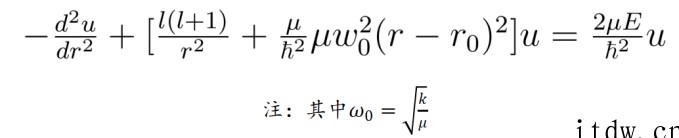
“这个方程有些难解。”张朝阳解释,由于原子核的振动距离非常小,并且转动能远远小于振动能,于是可以近似地将角动量项中的 r 直接换成平衡距离 r0,若定义新的参数为:
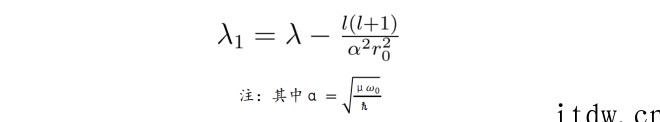
最终,薛定谔方程可以变形为:
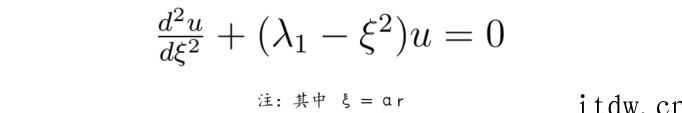
而这正是上节课解一维谐振子薛定谔方程时遇到过的微分方程。利用上节课的结论,马上能得到:
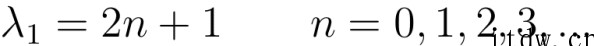
其对应的氢分子原子核的振动与转动能级就可以顺势求出:
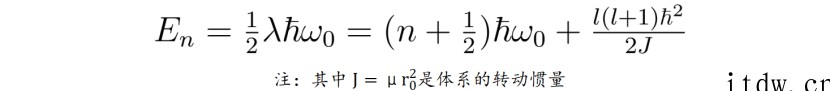

▲ (推导氢分子的振动转动能级)
氢分子的振动转动光谱:疏中有密,带状分布
“就像氢原子一样,一旦求出了氢分子原子核的振动与转动能级,就可以得出其对应的光谱。”张朝阳引导网友思考,“这里需要引入能级跃迁的选择定则。”也就是说,原子核跃迁前后的主量子数变化为 ±1,角量子数的变化也为 ±1。为了方便讨论,张朝阳还引入记号 B,将氢分子原子核的振动与转动能级写为:
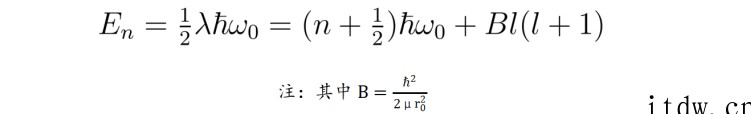
为了更方便地计算 B 的具体数值,张朝阳将 B 化为如下形式:
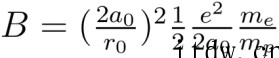
可以发现,关于电荷 e 的项正是氢原子的基态能量,这样代入对应数据非常容易求得 B=59 /cm。而为了对比转动能级与振动能级的量级差别,同样计算振动能级差对应的波数为 4000 /cm:
这样,明显看出转动能级与振动能级有巨大差距。为了更精确地得出能谱,现在考虑以主量子数和角量子数标记的能级的间距。E (n+1, l+1) 与 E (n , l) 能量相差:
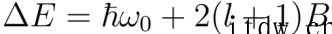
E (n+1 , l-1) 与 E (n , l) 能量相差:
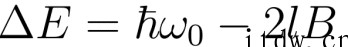
由于前面已经计算过,振动能级差远远大于转动能级差,综合上述跃迁的能级差,可知氢原子的光谱结构是以振动能级差为主,但周围有波数间距为 2B=120 /cm 的多条谱线。也就是说,整体上是在间距较大、相对稀疏的振动谱周围,辅以间距较小、相对密集的转动谱,最终观察到的是振-转光谱带。这与实验观测得到的氢分子光谱一致,再次证明了薛定谔方程的正确性与强大的功能。
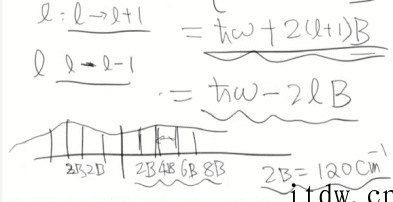
▲ (根据能级推导氢分子振动与转动光谱)
自 11 月 5 日至今,《张朝阳的物理课》已直播二十多期。在第一、二课中,张朝阳科普了“力”和“速度”,算出马斯克的飞船和中国空间站每日绕地飞行圈数;第三、四课和“振动”相关,科普可见光的基本知识;第五、六课引发了关于音速和温度的大讨论;在第七、八、九课重温经典物理学的两朵乌云。
第十、十一课重点回顾黑体辐射曲线及其应用;第十二、十三、十四课尝试进入爱因斯坦的思想世界,推导出著名的公式“E=mc²”,并论证钟慢尺缩效应;第十五课讲解了原子的结构和原子核的衰变;第十六课开始进入量子力学,讨论光的波粒二象性、康普顿散射、海森堡不确定性原理,以及薛定谔方程等。

1、IT大王遵守相关法律法规,由于本站资源全部来源于网络程序/投稿,故资源量太大无法一一准确核实资源侵权的真实性;
2、出于传递信息之目的,故IT大王可能会误刊发损害或影响您的合法权益,请您积极与我们联系处理(所有内容不代表本站观点与立场);
3、因时间、精力有限,我们无法一一核实每一条消息的真实性,但我们会在发布之前尽最大努力来核实这些信息;
4、无论出于何种目的要求本站删除内容,您均需要提供根据国家版权局发布的示范格式
《要求删除或断开链接侵权网络内容的通知》:https://itdw.cn/ziliao/sfgs.pdf,
国家知识产权局《要求删除或断开链接侵权网络内容的通知》填写说明: http://www.ncac.gov.cn/chinacopyright/contents/12227/342400.shtml
未按照国家知识产权局格式通知一律不予处理;请按照此通知格式填写发至本站的邮箱 wl6@163.com



