本篇文章给各位网友带来的资讯是:MIT 副教授赵宇飞团队“等角线”研究登数学四大顶刊之一:作者中两位是本科生,最小的是 00 后 详情请欣赏下文
你能想象,一个等角线问题,竟然困扰了数学家们 70 余年?
等角线的定义很简单,穿过一个点的一组直线,任 2 条之间夹角都相等就是等角线。
比如在二维平面相互垂直的两条直线或,或相互成 60 度角的 3 条直线。
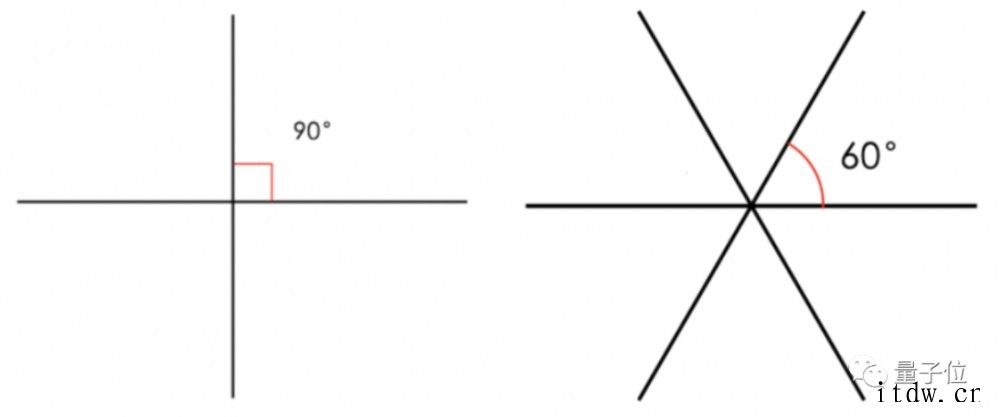
3 条直线形成的 6 个 60 度夹角,也刚好把一个二维空间分成 6 部分,合起来就是 360 度。
3 也就是二维空间中等角线数量的最大值了,很极限的满足了任意两条直线之间夹角都相等这个条件。
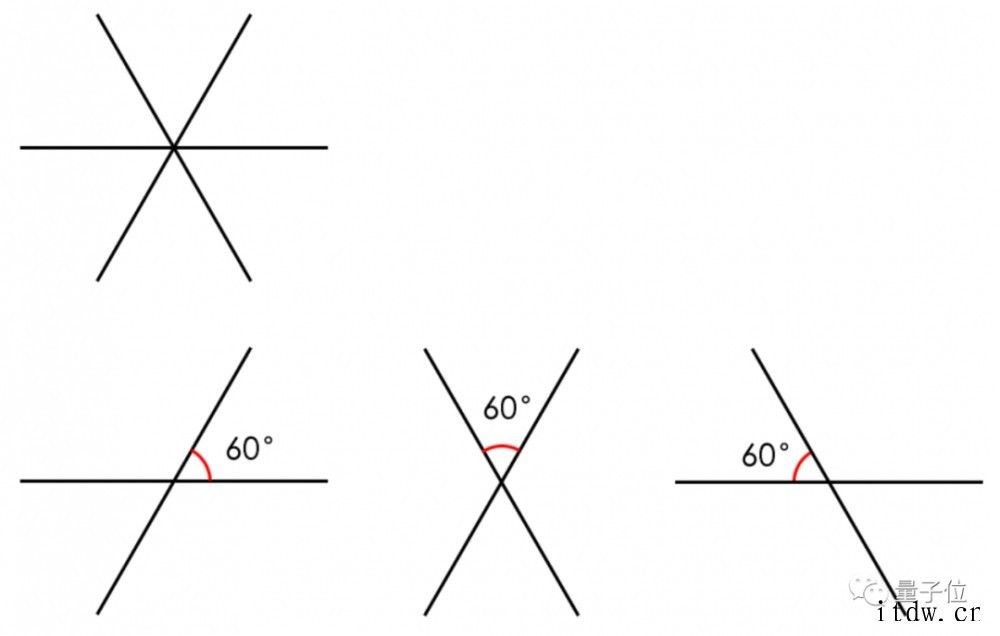
如果再多一条直线,无论怎么摆条件都无法成立。
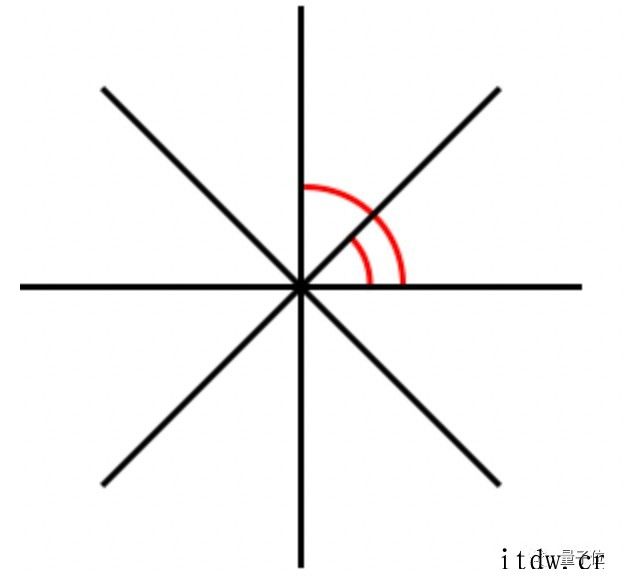
到了 3 维空间,情况要复杂一些,不过通过想象和画图也可以找出,等角线最多可以有 6 条,此时的夹角是 63.4 度。
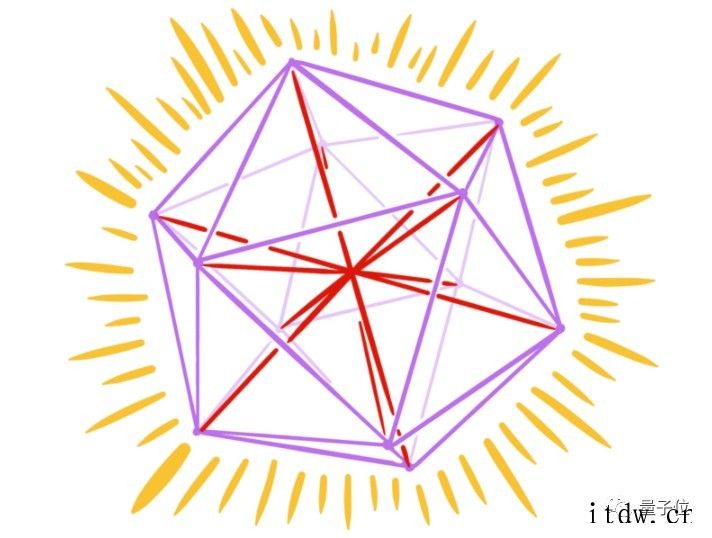
▲ 图源:MIT 作者:Zilin Jiang
到这里都还不难,然而推广到 4 维、5 维、6 维……N 维呢?
高维空间等角线数量最大值问题,一困扰数学家们就是几十年。
科学家们长久以来只能给出一个范围,而没办法算出精确的数值。
现在,这一难题终于被 MIT 副教授赵宇飞带领团队突破了,已被四大顶刊之一的《数学年刊》接受,预计于 2022 年的第一期发表。

普林斯顿大学教授 Noga Alon 对此评价:
这是一个美妙的结果,为几何极值中一个已经被广泛研究的问题提供了惊人的答案。
火星通信就用上了
在解答问题前,你可能有一个疑惑,研究这个做什么?
其实,寻找高维空间中的等角线最大值不仅有理论数学上的意义,也有一定的应用价值。
特别是嘈杂通信环境下的信息编码和传输问题。
比如正在遥远火星上探索的天问一号和祝融号,它们传回地球的信号该如何保证准确性?
信号在如此长的距离中传输,不可避免会遇到许多噪声。
像地球上飞机与塔台间的通信,手机移动信号等都会造成干扰,这样火星探测器发出的信号等传到地球早就变了样。
地球这边的接收方其实一直是靠猜去试图理解火星上传回的信息,这样问题就转化成了“发送方以什么形式编码信息,能让接收方更容易猜?”。
数学家们想到的一种办法,是把信息打包成“球形编码”,可以理解成把信息放在像经纬度一样的坐标点上。
关键在于只使用有限数量的点,只要不同点之间的距离足够远又有规律,接收一方就不容易把两个点的内容混淆。
只不过这里的球说的不是日常中能见到的三维球体,而是用数学描述的高维几何球体。
找到等角线就可以找出那些用来编码信息效果最好的点。
要理解这个问题,还是先回到简单的二维平面说起。
前面说到,二维平面上的等角线最多有 3 条,相互之间呈 60 度夹角。
用这 3 条直线可以构造出一个正六边形,它的 6 个顶点就适合用来构造球形编码(虽然在二维空间还只能叫圆形),相邻的点之间距离相等,经过噪声干扰后也不容易被误判成另一个点。
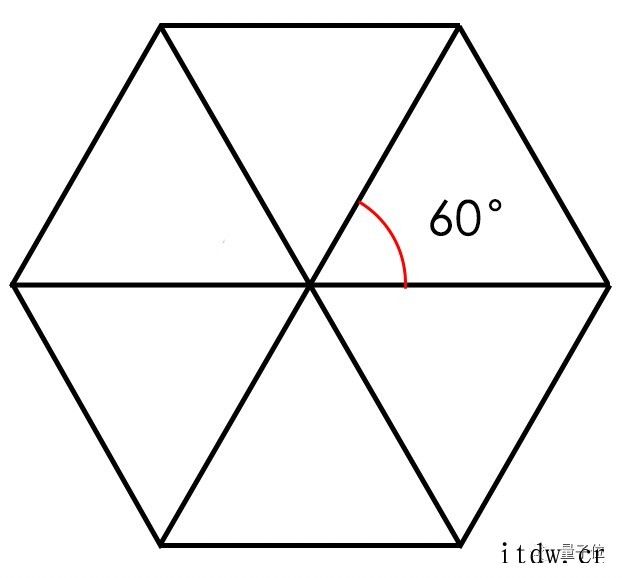
之所以要寻找等角线数量的最大值,是因为合适的点越多能发送的信息量也就越多。
如果换成三维,就是经过正二十面体中心的 6 条对角线。
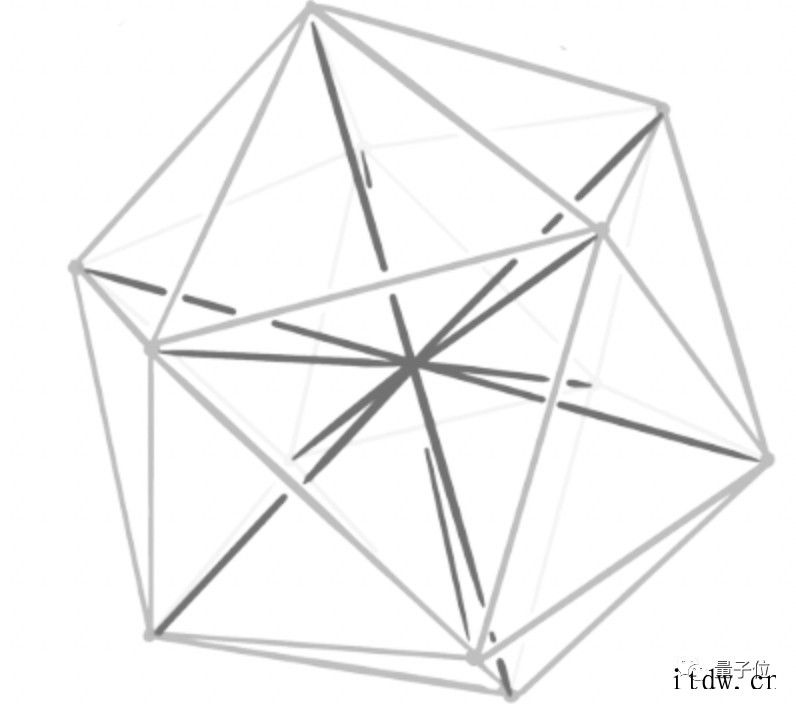
不过三维球形编码能发送的数据量,对于火星与地球间通信来说还是远远不够。
如何计算出更高维空间中等角线的最大值,就成了数学家们努力的目标。
用矩阵研究高维几何
很长一段时间里,数学家们能做到的就是证明等角线数量的最大值大致不能超过维度数的平方。
更具体一些,设维度数为 d,d 维空间的等角线数量最大值不能超过下面这个值:
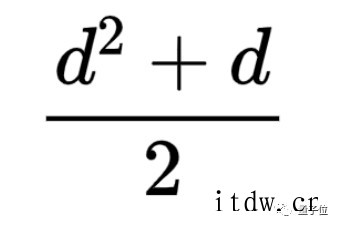
直到 2017 年,苏黎世联邦理工学院的 Benny Sudakov 教授的研究才在这一问题上取得了重要进展。
Sudakov 的方法是用线性代数和图论的方法来研究这个问题。
还是拿二维平面举例,先沿着每条线画一个单位向量:
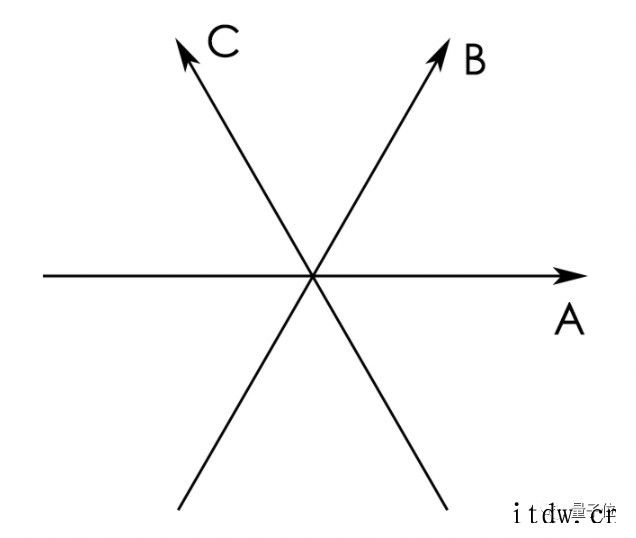
再去计算每两条向量之间的点积:
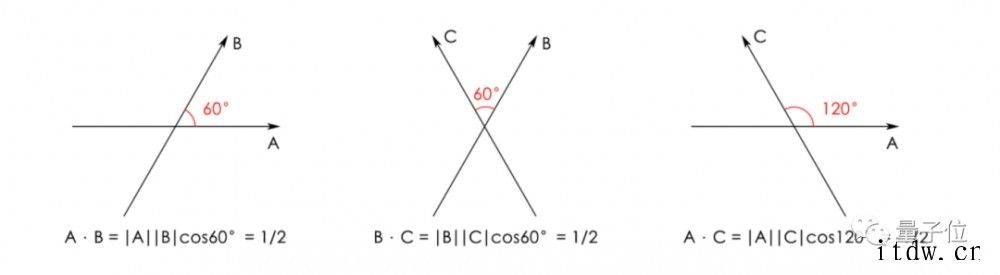
接下来需要图论的方法建立一个图,向量是图中的点。如果向量间的点积是正的,边就是红色;点积是负的,边就是蓝色。
进而可以用矩阵表示这个图:
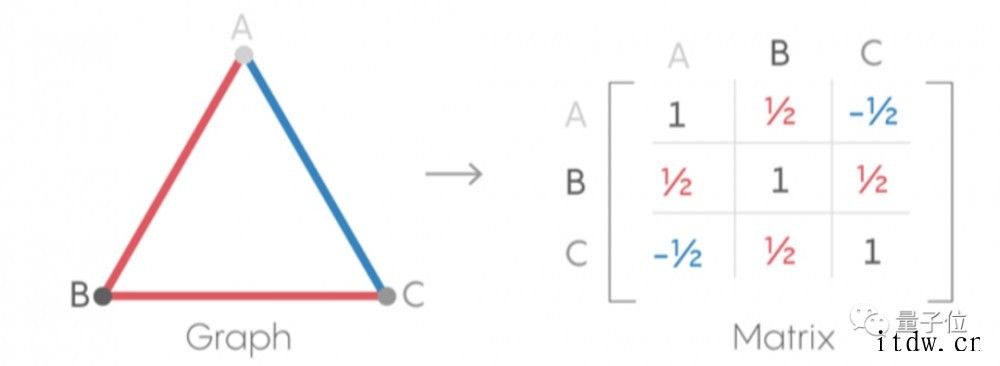
△图源:Quantum Magzine
高维等角线也可以按这个方法转换成矩阵表示,比如 5 维空间中的 8 个等角线:
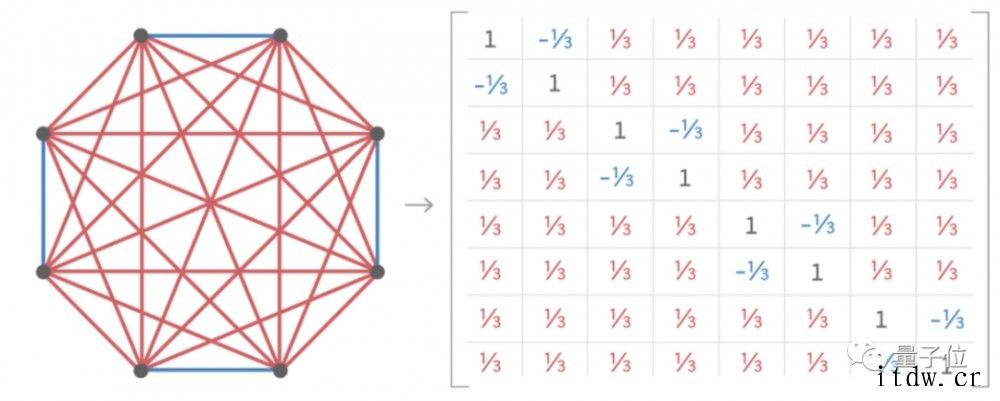
▲ 图源:Quantum Magzine
这样一个不直观、不方便研究的高维几何问题,就可以用上图论和线性代数里的诸多数学工具。
对于这种将高维几何问题转换的思路,西门菲沙大学的 Jonathan Jedwab 形容道:
这就像拿光照射 3 维物体,能看见它在一个方向的 2 维投影图;如果在光照下移动 3 维物体,就能比较不同方向得到的 2 维投影图,从而获得更多高维物体的信息。
在对这些矩阵进行研究的过程中,图论中的拉姆齐定理给了 Sudakov 灵感。
拉姆齐定理认为,找一个最小的自然数 R (k,l)=n ,使得 n 个人中必定有 k 个人互相认识或 l 个人互不相识。
这里的 k 和 l,刚好能和矩阵中的正负数对应起来,也就是上面图中的红色和蓝色。
通过将拉姆齐定理的相关结论灵活应用于等角线研究中,Sudakov 等人最终证明:
对任何 d 维的图,在特定角度(约 70.7°)下,等角线的最大数目是 2d-2;对于其他任何角度,等角线最大数目不超过 1.93d。
然而,这并不算是一个真正确定的结果,只是再次收紧了“等角线数量”的最大值范围。
现在,来自 MIT 的赵宇飞团队,利用一个发现的新定理,给出了这个难题的确定公式。
新定理解决 70 年难题
赵宇飞团队先是在对等角线进行研究中,发现并证明了一个新定理。
这个定理认为,有界度图(bounded degree graph)必须具有次线性第二特征值重数。
其中,度指在图论中,顶点相连接的边的数目,因此有限图一定是有界度图。
神奇的是,这个定理之前并没有人给出过,但发现它也确实需要非常的洞察力。
依据发现的新定理,赵宇飞团队成功解决了这个 70 年一直悬而未解的问题:
在给定角度的情况下,所有足够大的任意维度空间中,等角线数量的最大值是多少。
具体来说,这篇论文的结论如下:
给定数值 α 满足 0<α<1,计算出给定角度 arccos α,设 d 维图中等角线数量的最大值为。
设 k 代表邻接矩阵谱半径为 (1 − α)/(2α) 的图的最小顶点数。
如果 k<∞,那么对于所有足够大的 d,都有:
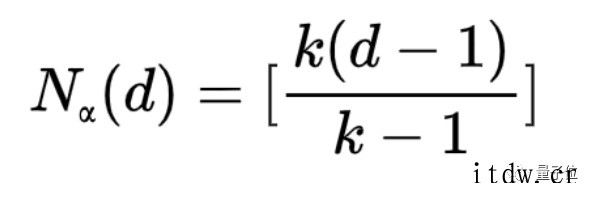
否则有:
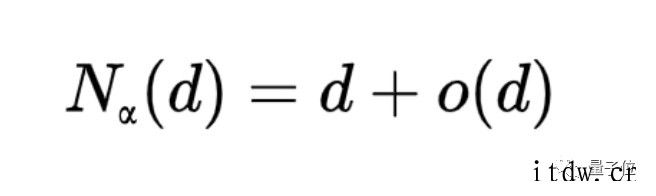
特殊地,在 k (k 为整数)≥2 的情况下,对于所有足够大的 d,有:
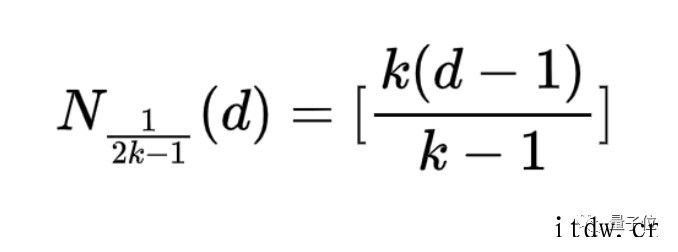
在此之前,数学家们的研究一直都停留在研究最大值的范围上,没有人能给出在指定角度下,任意维度的等角线数量最大值的确定公式。
对于这项研究,赵宇飞表示:
当时我有预感,团队会在等角线上取得一些不错的进展,但完全解决整个问题还是超出了我的预期。
本来是学生暑期项目,最小作者 00 后
这次论文背后的团队导师赵宇飞(Yufei Zhao),在武汉出生,1999 年随父母移民加拿大。
据中新网报道,赵宇飞在中学时被选入资优班,他的数学老师表示“15 年间,从未给过学生满分,直至遇到他”。
目前,赵宇飞在 MIT 任助理教授。

他在 MIT 获得数学和计算机科学双学士学位后,于剑桥大学取得硕士学位,并于 2015 年获 MIT 博士学位。
在求学期间,赵宇飞深入研究了大图(足够大的图 graph)的规律,尤其是对其中的“图正则引理”进行了深入研究。
他认为,在图数据越来越庞大的当下,大图的世界是无限的,而图正则原理、图极限等数学方法,正是解决图数据问题的重要工具。
也正是基于这一领域的研究成果,赵宇飞获得了有“诺奖风向标”之称的斯隆奖、柯尼希奖(König Prize )和 MIT 未来科学家奖。

虽然他的主要研究领域是加性组合,不过他兴趣广泛,对极值问题和概率论,以及理论计算机科学中的很多问题都感兴趣。
值得注意的是,赵宇飞的学生 Ashwin Sah 在本科期间,还曾经对本次研究用到的拉姆齐数理论做出过重要突破。
这次与等角线最大值问题结缘,是从 2018 年先在这一问题作出突破的 Sudakov 教授到 MIT 访问交流开始。
赵宇飞是那次交流活动的主持人。
Sudakov 研究这一问题是受卡耐基梅隆大学的一位学者 Bukh Boris 启发,而本次研究的另一位作者博士后姜子麟在博士时的导师正是 Boris。
到了 2019 年暑期,赵宇飞和姜子麟带着共同的兴趣将这一课题作为 MIT 数学系暑期研究项目开展。
学生中的 3 人张盛桐、姚远和 Jonathan Tidor 参与了这个项目,5 人组成了研究小组。
一开始他们只是觉得这个问题足够大,是一个暑期研究的好项目,也没想着能取得多大进展。
没想到,最后直接一举解决了。

合影里中间一位是赵宇飞。
左数第一位姜子麟,北大数院校友,CMU 博士,以色列理工学院博士后,发表这篇论文期间,他曾经在 MIT 进行博士后工作。
2017 年,他曾经与 MIPT 的 Alexandr Polyanskii 证明了离散几何中的一个重要猜想“球带猜想”(Zone Conjecture),解决了困扰数学家们长达四十余年的问题。
左数第二位是 Jonathan Tidor,现 MIT 博士生,主要研究方向是加性组合、高阶傅里叶分析和离散几何。
右数第二位姚远,上外附中校友,目前是 MIT 研究生,2016 年美国队 IMO 金牌满分选手,连续两届获得阿里全球数学竞赛优秀奖和铜奖,普特南大学生数学竞赛特等奖(fellow)。
右数第一位张盛桐,上海中学校友,MIT 本科生(2000 年出生),连续三届获得阿里全球数学竞赛银奖、2016 年国家队 IMO 金牌,有“加强版 IMO”之称的普特南大学生数学竞赛特等奖(fellow)。
据赵宇飞教授 2019 年的博客,发表这篇文章时,姚远和张盛桐分别都还是 MIT 的本科生,其中姚远就读大二,张盛桐则刚上大一:

本科生阶段的研究成果就登上四大顶刊之一《数学年刊》,也是很厉害了。

1、IT大王遵守相关法律法规,由于本站资源全部来源于网络程序/投稿,故资源量太大无法一一准确核实资源侵权的真实性;
2、出于传递信息之目的,故IT大王可能会误刊发损害或影响您的合法权益,请您积极与我们联系处理(所有内容不代表本站观点与立场);
3、因时间、精力有限,我们无法一一核实每一条消息的真实性,但我们会在发布之前尽最大努力来核实这些信息;
4、无论出于何种目的要求本站删除内容,您均需要提供根据国家版权局发布的示范格式
《要求删除或断开链接侵权网络内容的通知》:https://itdw.cn/ziliao/sfgs.pdf,
国家知识产权局《要求删除或断开链接侵权网络内容的通知》填写说明: http://www.ncac.gov.cn/chinacopyright/contents/12227/342400.shtml
未按照国家知识产权局格式通知一律不予处理;请按照此通知格式填写发至本站的邮箱 wl6@163.com



