60多年悬而未决,中国科大陈秀雄团队成功证明凯勒几何两大核心

本篇文章给各位网友带来的资讯是：60 多年悬而未决，中国科大陈秀雄团队成功证明凯勒几何两大核心猜想 详情请欣赏下文

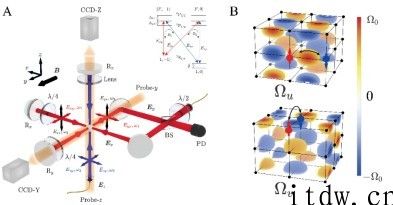
IT大王 11 月 2 日消息，中国科学技术大学宣布，该校几何物理中心创始主任陈秀雄教授与合作者程经睿在偏微分方程和复几何领域取得“里程碑式结果”，他们解出了一个四阶完全非线性椭圆方程，成功证明“强制性猜想”和“测地稳定性猜想”这两个国际数学界 60 多年悬而未决的核心猜想，解决了若干有关凯勒流形上常标量曲率度量和卡拉比极值度量的著名问题。

据介绍，凯勒流形上常标量曲率度量的存在性，是过去 60 多年来几何中的核心问题之一。关于其存在性，有三个著名猜想 —— 稳定性猜想、强制性猜想和测地稳定性猜想。稳定性猜想限制在凯勒-爱因斯坦度量时称为丘成桐猜想，由著名华裔数学家丘成桐于 20 世纪 90 年代提出，并由陈秀雄、唐纳森和孙崧率先解决。经过近 20 年众多著名数学家的工作，强制性猜想和测地稳定性猜想中的必要性已变得完全清晰，但其充分性的证明在陈-程的工作之前被认为遥不可及，就如同不带任何装备攀登高峰一般艰难。

求出一类四阶完全非线性椭圆方程的解，就能证明常标量曲率度量的存在性。陈-程的工作恰恰就是在 K-能量强制性或测地稳定性的假设下，证明了这类方程解的存在。这类方程的研究极为困难，长期以来业内专家普遍不相信会有一个令人满意的存在性理论。在陈-程的工作前，对此类方程几乎没有合适的处理工具。陈-程最重要的突破是给出了这类方程的先验估计以及成功实现了陈秀雄教授提出的新的连续参数的策略。

专家认为，求解一类四阶完全非线性椭圆方程，此前就如同一块无形的幕墙挡在数学家面前，陈-程的工作就是在幕墙上“掏了一个洞”，在毫无征兆的情况下找到一个突破口，不仅求出了方程的解，而且建立了一套系统研究此类方程的方法，为探索未知的数学世界提供了一种新工具。

IT大王了解到，两篇论文日前发表于国际著名刊物《美国数学会杂志》。