左导数在哪(左导数不等于右导数那么该处导数是否存在)

瞬时速度与曲线斜率

对于动态问题左导数在哪：非匀速运动物体左导数在哪，某一时刻的瞬时速度

运动物体的瞬时速度

对于静态问题左导数在哪：曲线某一点的斜率

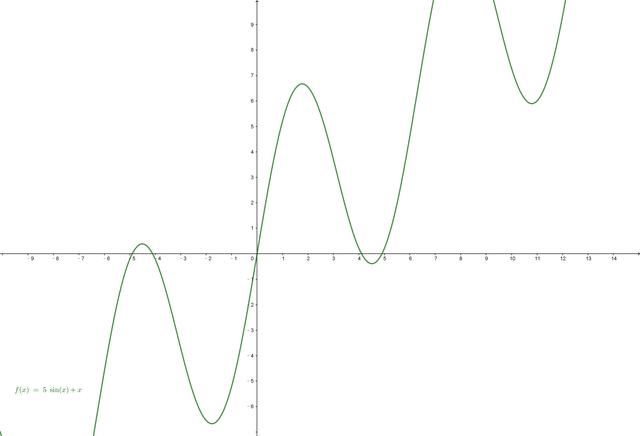
曲线图像

以上两个问题，让我们对细微之处的变化产生了兴趣。

数学家们已经给出问题的答案：

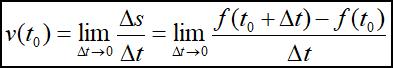
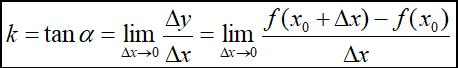函数在一点处的导数

函数y=f(x)在点x0的某领域内有定义，当x在点x0处取得增量△x，y取得相应增量△y，若下列极限存在：

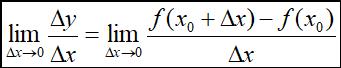
则称f(x)在点x0处可导，且此极限值称为f(x)在点x0处的导数，记为：

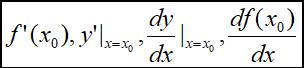
导数的符号

即：

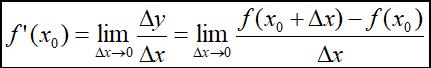
若令x=x0+△x，则可写为：

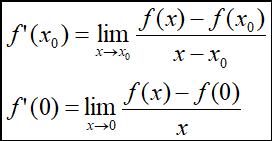
若上式极限不存在，或者无穷大，则称f(x)在点 x0不可导。

单侧导数

若极限

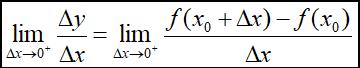
存在，则称此极限值为f(x)在点x0的右导数，记为：

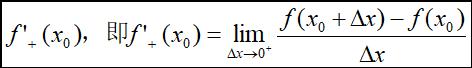
右导数记号

同理有左导数：

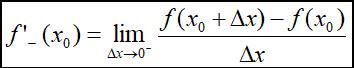
左导数

导数的关系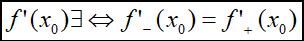

导数存在充要条件

函数在区间上的可导性

若函数f(x)在(a,b)内每一点都是可导的，则称f(x)在(a,b)内是可导的。若f(x)在(a,b)内可导，且f(a)的右极限，f(b)的左极限都存在。则称f(x)在[a,b]内是可导的。

导函数

若f(x)在某区间I可导，对区间I内任一x，都有唯一导数与之对应，我们可以得到导函数，记为：

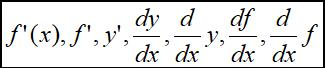
导数